Трехмерные фрактальные ландшафты
Джон ШемитцПолотна великих сюрреалистов вам не по карману? Тогда создайте виртуальный сюрреалистический пейзаж по своему вкусу (ведь он может быть сколь угодно велик). Для этого потребуется лишь фрактальная технология и немножко старой доброй магии Delphi.
Слово «фрактал» я впервые услышал примерно в 1983 году, когда еще занимался программированием больших компьютеров. Мы с коллегой обсуждали только что полученные IBM PC, и он спросил, нет ли у меня программ для расчета фракталов.
«Нет», — ответил я. — «А что такое фракталы?»
Он объяснил, что фрактальное изображение создается применением некоторой геометрической операции к простой фигуре и последующим многократным применением той же операции к полученному результату. Хотя такое объяснение совершенно не затрагивает тех замечательных свойств фракталов, которые так интересуют математиков, оно вполне грамотно описывает, как же фракталы генерируются.
Несомненно, в полной мере это относится и к построению трехмерных фрактальных ландшафтов.
Разделяй и сгибай
Чтобы сгенерировать ландшафт, достаточно присвоить случайные высоты трем вершинам равностороннего треугольника, а затем «изогнуть» каждое ребро, поднимая или опуская его середину на случайную величину. Соедините линиями середины трех сторон — исходный треугольник разделится на четыре треугольника. Если теперь применить операции изгиба и деления к каждому из получившихся треугольников, то вскоре у вас получится нечто, невероятно похожее на реальный ландшафт (см. рис. 8.1, 8.2 и 8.3).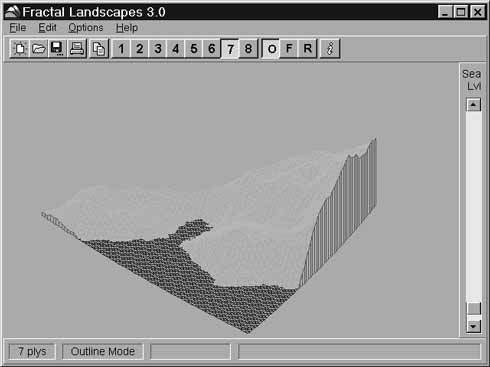
Рис. 8.1. Каркасный фрактальный ландшафт
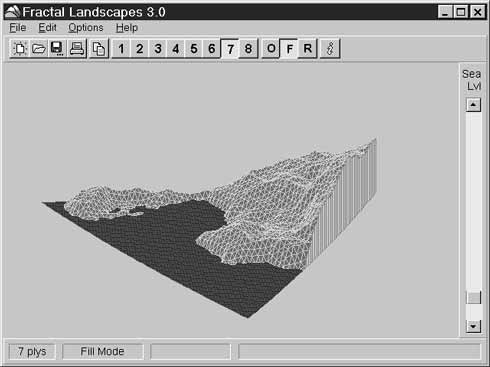
Рис. 8.2. Фрактальный ландшафт с заполнением
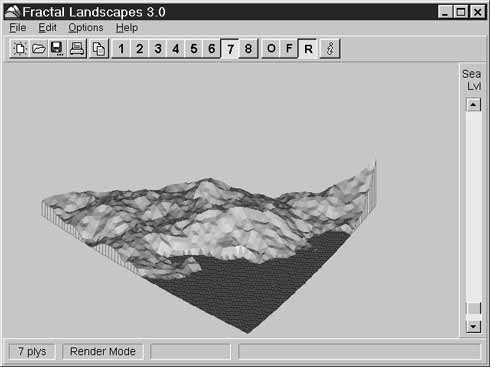
Рис. 8.3. Фрактальный ландшафт со светотенью
Проблема общих сторон
Конечно, в действительности генерация фрактальных ландшафтов не сводится к примитивному рецепту «изогнуть, разделить, повторить по вкусу». Вам придется проследить за тем, чтобы каждая линия изгибалась только один раз; к тому же ландшафт еще необходимо отобразить на экране, но это уже подробности.Первая и самая важная деталь заключается в том, что вы должны следить за своими действиями. Если процедура FractureTriangle() будет просто изгибать все грани подряд, у вас получится что-то вроде рис. 8.4. Треугольники не будут образовывать сплошную сетчатую поверхность; появятся «плавающие» группы из четырех треугольников, высота вершин которых не будет совпадать с высотой вершин соседей.
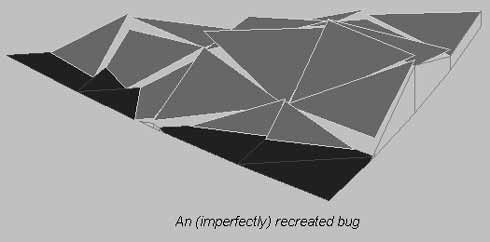
Рис. 8.4. Вот что получается, когда стороны не совпадают
Возможно, рис. 8.5 поможет разобраться в происходящем. Внутренние стороны принадлежат сразу двум треугольникам, мнения которых насчет величины изгиба могут не совпасть. Вершина I является серединой отрезка DF, который принадлежит треугольникам CDF и DEF. Если оба треугольника попытаются самостоятельно задать высоту этой точки, то вершина I в треугольниках 1, 2 и 3 будет находиться на иной высоте, чем она же в треугольниках 4, 5 и 6!
Очевидно, нам потребуется база данных вершин, чтобы положение вершины I можно было задать при обработке треугольника CDF и затем использовать ту же величину смещения для этой вершины при обработке треугольника DEF. Можно попытаться объявить DEF «внутренним» треугольником, рассматривать его в последнюю очередь и использовать «внешние» значения для вершин G, H и I — но взгляните на треугольники GEH и LMN. Отрезки GE и EH принадлежат и «внешним» треугольникам, поэтому для вершин L и M следует использовать «внешние» значения, но отрезок GH находится «полностью внутри», поэтому его необходимо изогнуть. Несомненно, схему с внешними и внутренними треугольниками можно усовершенствовать для правильной обработки таких «внешне-внутренних субтреугольников», но в итоге получится нечитаемый код с высокой вероятностью возникновения ошибок при любых изменениях.
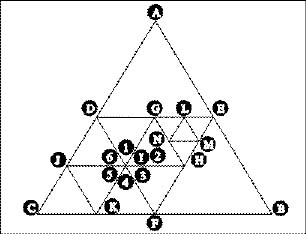
Рис. 8.5. Так треугольники «спорят» из-за вершин
Намного проще определить специальное значение координаты, которое будет присутствовать только у неинициализированных вершин, и заставить FractureTriangle() проверять, не было ли положение середины отрезка задано ранее. Если положение уже задано, FractureTriangle() использует готовое значение; если нет, FractureTriangle() генерирует новую высоту. Возможно, вычисление и просмотр середин внутренних треугольников работают несколько медленнее, чем простая передача аргументов, но программа получается более компактной и наглядной. К тому же на отображение ландшафта неизбеж но уйдет намного больше времени, чем на его расчет.
Треугольный массив
При изгибании отрезка мы изменяем лишь z-координату его середины, поэтому теоретически можно использовать пару координат [x, y] как индекс в таблице со значениями z. Однако такой массив получится весьма разреженным, а с нормальным, непрерывным массивом программа работает намного быстрее — ей не приходится тратить время на просмотр списков разреженного массива. Именно по этой причине в листинге 8.1 определена система двумерных логических адресов (тип данных TVertex), в которые «отображаются» фактические трехмерные координаты (тип данных Ttriple).Листинг 8.1. Модуль GLOBAL.PAS
unit Global;
{Fractal Landscapes 3.0 - Copyright ©
1987..1996, Джон Шемитц}
interface
uses WinTypes;
type
Int16 = {$ifdef Ver80} integer {$else}
SmallInt {$endif} ;
const
MaxPlys = 8;
MaxEdgeLength = 1 shl (MaxPlys - 1);
UnitLength: LongInt = 5000;
ShadesOfGray = 64;
type
TCoordinate = -30000..30000;
TTriple = record
X, { Ширина: от 0 (слева) до UnitLength
(справа)}
Y, { Глубина: от 0 (спереди) до
VanishingPoint.Y (сзади)}
Z: TCoordinate; { Высота: от 0 (снизу) до
UnitLength (сверху)}
end;
function Triple(X, Y, Z: TCoordinate): TTriple;
type
TPixel = TPoint;
type
GridCoordinate = 0..MaxEdgeLength;
{ Треугольная сетка }
TVertex = record
AB, BC, CA: GridCoordinate;
end;
function Vertex(AB, BC, CA: GridCoordinate):
TVertex;
type
DrawModes = (dmOutline, dmFill, dmRender);
DrawRates = (drLow, drMedium, drHigh);
const
Envelope = 3000;
SeaLevel: word = 100; { от 0 (снизу) до
UnitLength (сверху)}
VanishingPoint: TTriple = ( X: 1500 ;
Y: 25000 ;
{ Видимая глубина точки перспективы }
Z: 15000 );
LightSource: TTriple = ( X: 2500;
Y: +7500;
Z: 25000 );
DrawMode: DrawModes = dmOutline;
DrawRate: DrawRates = drHigh;
const
Uninitialized = -30000;
var
A, B, C: TVertex;
Plys: 1..MaxPlys;
EdgeLength: Int16;
DisplayHeight,
DisplayWidth: Int16;
implementation
function Triple(X, Y, Z: TCoordinate): TTriple;
begin
Result.X := X;
Result.Y := Y;
Result.Z := Z;
end;
function Vertex(AB, BC, CA: GridCoordinate):
TVertex;
begin
Result.AB := AB;
Result.BC := BC;
Result.CA := CA;
end;
end.
Вероятно, простейшая схема такого отображения заключается в нумерации всех вершин вдоль каждой из трех сторон внешнего треугольника (см. левую половину рис. 8.6) и использовании всех трех координат для вершин каждой стороны. Хотя в действительности нам нужны лишь две координаты, а третья избыточна, я предпочитаю ссылаться на внешние вершины треугольника в чуть более понятном виде [1, 0, 0], [0, 1, 0] и [0, 0, 1] вместо [1, 0], [0, 1] и [0, 0]. Именно по этой причине тип TVertex определяется в виде тройки координат, несмотря на то что третья координата в принципе не нужна и даже слегка замедляет вычисления.
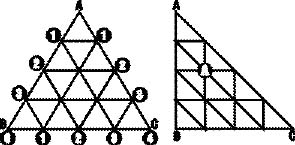
Рис. 8.6. Сохранение вершин в «квадратном» массиве
Впрочем, когда дело доходит до базы данных вершин, третья координата действительно игнорируется. Как видно из правой половины рис. 8.6, координаты вершин сохранятся и в том случае, если равносторонний треугольник преобразовать в прямоугольный. Поэтому координаты AB и BC можно будет использовать так, словно они относятся к элементу «квадратного» массива.
Однако сохранение нашего «треугольного» массива в «квадратном» означало бы, что почти половина места в массиве пропадает даром. В принципе в этом нет ничего страшного, хотя в 16-разрядной среде мы бы столкнулись с ограничением на размер сегмента (64 Кб). Каждый элемент типа TTriple состоит из трех 16-разрядных чисел с фиксированной точкой, поэтому квадратный массив после восьми итераций деления сторон (рис. 8.7) будет содержать (28-1 + 1)2 вершин, или 99 846 байтов. Если же сохранять только вершины, принадлежащие диагонали или находящиеся под ней, объем сокращается до 50 310 байтов. В этом случае можно воспользоваться простым индексированием вместо huge-указателей и массивов. К тому же вся база данных (по крайней мере в данной демонстрационной программе) помещается в одном сегменте данных, что ускоряет доступ к ней по сравнению с дополнительным выделением блоков из пула и использованием указателей.
Поскольку восемь итераций вряд ли можно назвать слишком мелким делением для экрана 1280?1024, описанная в этой главе программа Fractal Landscapes 3.0 (она же FL3 — переработанная (сначала под Windows, а затем для Delphi) версия DOS-программы, изначально написанной «для души» на Turbo Pascal 4.0) использует «треугольную» структуру базы данных (см. листинг 8.2). Основная идея заключается в том, что каждый ряд вершин хранится в базе после предыдущего ряда. Поскольку первый ряд состоит всего из одной вершины, второй ряд начинается со второй «ячейки». Он состоит из двух вершин, поэтому третий ряд начинается с четвертой ячейки, и так далее.
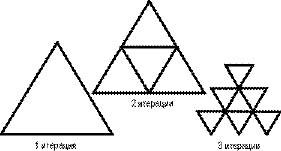
Рис. 8.7. Процесс многократного деления
Листинг 8.2. Модуль DATABASE.PAS
unit Database;
{ Fractal Landscapes 3.0 -
Copyright © 1987..1997, Джон Шемитц }
{ База данных и генерация ландшафта }
interface
uses SysUtils, Global;
{ Вспомогательные математические функции }
function IDIV(Numerator: LongInt; Denominator:
Int16): Int16;
{$ifdef Ver80} {В Delphi 1.0 еще поддерживаются
InLine-функции}
InLine(
$5B / { POP BX ; Делитель }
$58 / { POP AX ; Младшее слово делимого }
$5A / { POP DX ; Старшее слово делимого }
$F7 / $FB { IDIV BX ; Частное }
{$endif}
function IMUL(A, B: Int16): LongInt;
{$ifdef Ver80} {В Delphi 1.0 еще
поддерживаются InLine-функции}
InLine(
$5B / { POP BX }
$58 / { POP AX }
$F7 / $EB { IMUL BX }
);
{$endif}
function Rand(Envelope: integer): integer;
{ База данных }
procedure ResetDB;
function GetTriple(const V: TVertex): TTriple;
{ DB[V] }
procedure SwapTriples(var A, B: TTriple);
function Midpoint(A, B: TVertex): TVertex;
function LoadLandscape(const FileName: TFileName)
: boolean;
function SaveLandscape(const FileName: TFileName)
: boolean;
{ Вычисления }
procedure FractureTriangle(const A, B, C:
TVertex; Plys: word);
function Unscale(ScaledCoordinate: LongInt):
TCoordinate;
{$ifdef Ver80} {В Delphi 1.0 еще поддерживаются
InLine-функции}
InLine(
$58 / { POP AX ; младшее слово SC }
$5A / { POP DX ; старшее слово SC }
$8B / $1E / UnitLength /
{ MOV BX,[UnitLength] ; младшее слово
масштабного
коэффициента}
$F7 / $FB { IDIV BX ; Обратное
масштабирование }
);
{$endif}
implementation
{ Вспомогательные математические функции }
{$ifNdef Ver80}
{ В 32-разрядных версиях Delphi InLine-функции
не поддерживаются }
function IDIV(Numerator:
LongInt; Denominator: Int16): Int16;
begin
Result := Numerator div Denominator;
end;
{$endif}
{$ifNdef Ver80}
{ В 32-разрядных версиях Delphi InLine-функции
не поддерживаются }
function IMUL(A, B: Int16): LongInt;
begin
Result := Longint(A) * B;
end;
{$endif}
function Rand(Envelope: integer): integer;
{ Псевдонормальное распределение
в интервале ±Envelope }
begin
Rand := integer(Random(Envelope)) +
integer(Random(Envelope)) -
Envelope;
end;
{$ifNdef Ver80}
{В 32-разрядных версиях Delphi
InLine-функции не поддерживаются }
function Unscale(ScaledCoordinate: LongInt):
TCoordinate;
begin
Result := ScaledCoordinate div UnitLength;
end;
{$endif}
{ База данных }
var
DB: array[0..8384] of TTriple;
{ Треугольный массив: (MEL+1) элементов }
NumberOfVertices, TopRow: word;
Envelopes: array[1..MaxPlys] of word;
function Vertices(N: word): word;
{ Число вершин, содержащихся в
равностороннем треугольнике
с длиной стороны N-1 }
begin
Vertices := (Sqr(N) + N) shr 1;
end;
function Midpoint(A, B: TVertex): TVertex;
begin
Result := Vertex( (A.AB + B.AB) shr 1,
{ среднее }
(A.BC + B.BC) shr 1,
(A.CA + B.CA) shr 1 );
end;
function Loc(const V: TVertex): word;
begin
Loc := NumberOfVertices -
Vertices(TopRow - V.AB) + V.BC;
{ ^^^^^^^^^^^^^^^^^^
На самом деле это не нужно и приводит
к напрасным затратам времени,
но сохранено для совместимости
с .FL-файлами программы FL2. }
end;
procedure SetTriple(var V: TVertex;
var T: TTriple); { DB[V] := T }
begin
DB[Loc(V)] := T;
end;
function GetTriple(const V: TVertex):
TTriple; { DB[V] }
begin
Result := DB[Loc(V)];
end;
procedure SwapTriples(var A, B: TTriple);
var
Tmp: TTriple;
begin
Tmp := A; A := B; B := Tmp;
end;
procedure SwapZ(var A, B: TTriple);
var
C: TCoordinate;
begin
C := A.Z; A.Z := B.Z; B.Z := C;
end;
const
Uninitialized = -30000;
procedure ResetDB;
var
T: TTriple;
R, Theta: double;
I, Offset: integer;
tA, tB, tC: TTriple;
const
Base_Rotation = - Pi / 2.1; { Поворот
против часовой стрелки }
RotateBy = Pi * 2 / 3; {120°}
begin
{ Установить параметры, зависящие от числа
итераций (Plys) }
EdgeLength := 1 shl (Plys - 1);
TopRow := EdgeLength + 1;
{ "Ограничитель" }
NumberOfVertices := Vertices(TopRow);
for I := Plys downto 1 do
Envelopes[I] := Envelope shr Succ(Plys - I);
{ Сбрасываем в исходное состояние
NumberOfVertices вершин в базе данных }
T.X := Uninitialized;
T.Y := Uninitialized;
T.Z := Uninitialized;
for I := Low(DB) to High(DB) do DB[I] := T;
{ Теперь задаем положение
"определяющих" (то есть внешних)
точек A, B и C }
A.AB := 0; A.BC := EdgeLength;
\A.CA := 0;
B.AB := 0; B.BC := 0;
B.CA := EdgeLength;
C.AB := EdgeLength; C.BC := 0;
C.CA := 0;
{ Рассчитываем для них тройки координат }
Offset := UnitLength div 2;
R := UnitLength / 2;
Theta := Base_Rotation;
tA := Triple( Round(R * Cos(Theta)) + Offset,
Round(R * Sin(Theta)) + Offset,
SeaLevel + Rand(Envelope) );
Theta := Theta + RotateBy;
tB := Triple( Round(R * Cos(Theta)) + Offset,
Round(R * Sin(Theta)) + Offset,
SeaLevel + Rand(Envelope) );
Theta := Theta + RotateBy;
tC := Triple( Round(R * Cos(Theta)) + Offset,
Round(R * Sin(Theta)) + Offset,
SeaLevel + Rand(Envelope) );
{ По крайней мере одна точка должна
находиться над уровнем моря }
if (tA.Z < SeaLevel) AND (tB.Z <
SeaLevel) AND (tC.Z < SeaLevel) then
repeat
tB.Z := SeaLevel + Rand(Envelope);
until tB.Z > SeaLevel;
{ Сделаем A самой нижней точкой... }
if tA.Z > tB.Z then SwapZ(tA, tB);
if tA.Z > tC.Z then SwapZ(tA, tC);
SetTriple(A, tA);
SetTriple(B, tB);
SetTriple(C, tC);
end;
function SaveLandscape(const FileName:
TFileName): boolean;
var
Handle: integer;
begin
try
Handle := FileCreate(FileName);
try
Result :=
(FileWrite(Handle, Plys, SizeOf(Plys))
= SizeOf(Plys))
and
(FileWrite(Handle, DB,
NumberOfVertices * SizeOf(TTriple))
= NumberOfVertices * SizeOf(TTriple));
finally
FileClose(Handle);
end;
except
on Exception {любое исключение}
do Result := False;
end;
end;
function LoadLandscape(const FileName:
TFileName): boolean;
var
Handle: integer;
begin
Result := False;
try
Handle := SysUtils.FileOpen(FileName,
fmOpenRead);
try
if FileRead(Handle, Plys, SizeOf(Plys))
= SizeOf(Plys) then
begin
ResetDB;
LoadLandscape := FileRead( Handle, DB,
NumberOfVertices * SizeOf(TTriple))
= NumberOfVertices * SizeOf(TTriple);
end;
finally
FileClose(Handle);
end;
except
on Exception {любое исключение}
do Result := False;
end;
end;
{ Основные действия }
procedure FractureLine( var vM: TVertex;
const vA, vB: TVertex;
Envelope: integer );
var
A, B, M: TTriple;
begin
vM := Midpoint(vA, vB);
M := GetTriple(vM);
if M.X = Uninitialized then { Еще не задано }
begin
A := GetTriple(vA); B := GetTriple(vB);
M := Triple( A.X + (B.X - A.X) div 2,
A.Y + (B.Y - A.Y) div 2,
A.Z + (B.Z - A.Z) div 2 + Rand(Envelope) );
{ Средняя высота ± Random(Envelope) }
SetTriple(vM, M);
end;
end;
procedure FractureTriangle(const A, B, C:
TVertex; Plys: word);
var
Envelope: word;
AB, BC, CA: TVertex;
begin
if Plys > 1 then
begin
Envelope := Envelopes[Plys];
FractureLine(AB, A, B, Envelope);
FractureLine(BC, B, C, Envelope);
FractureLine(CA, C, A, Envelope);
Dec(Plys);
FractureTriangle(CA, BC, C, Plys);
FractureTriangle(AB, B, BC, Plys);
FractureTriangle(BC, CA, AB, Plys);
FractureTriangle(A, AB, CA, Plys);
end;
end;
end.
Изгибы
Существует и другая тонкость, которую я обнаружил лишь после написания программы, — при изгибе длинных линий нельзя использовать ту же величину случайных отклонений, что и для коротких. В противном случае получает ся равнина, усеянная кочками, или «гребенка» из сплошных пиков. Амплитуда случайных трансформаций должна увеличиваться для внешних треугольни ков, определяющих общую форму ландшафта, и уменьшаться для внутрен них треугольников, определяющих тонкую структуру поверхности.В итоге у меня получилась функция, которая
генерирует нечто, отдаленно похожее на нормальное распределение:
function Rand(Envelope: integer): integer;
{ Псевдонормальное распределение в интервале
±Envelope }
begin
Rand := integer(Random(Envelope)) +
integer(Random(Envelope)) -
Envelope;
end;
В нашем случае значение Envelope для каждой итерации равно половине стороны отрезка, полученного на предыдущей итерации. Конечно, в результате получаются вполне приемлемые пейзажи, однако настоящий ландшафт обычно выглядит не так гладко, как нарисованный программой FL3. В настоящих ландшафтах встречаются острые края — скалы, плоскогорья, ущелья и т. д., тогда как FL3 способна сгенерировать разве что крутой склон.
Возможный выход заключается в том, чтобы заменить псевдонормальное распределение Rand экспоненциальным. Для малых отрезков такая функция будет с большей вероятностью порождать близкие к нулю значения, чем для больших, но возможность случайного выброса останется при любом значении параметра Envelope.
Сначала построить, потом выводить
В первом воплощении этой программы за отображение ландшафта отвечала та же рекурсивная функция, в которой он рассчитывался. Если аргумент Plys (число итераций) превышал 1, функция разбивала полученный в качестве параметра треугольник на четыре новых, затем уменьшала Plys и вызывала себя для каждого из полученных треугольников. Когда аргумент Plys достигал 1, вызывалась функция, которая рисовала треугольник на экране.Такой алгоритм выглядит достаточно просто, но при переходе от «каркасного» отображения к заполненным треугольникам приходилось заново генерировать весь ландшафт. Кроме того, применение этого алгоритма в Windows-программе означает, что ландшафт будет заново генерироваться при каждом изменении размеров окна. Очевидно, более разумный подход — сначала рассчитать ландшафт, а затем вывести его на экран. Это потребует проведения двух независимых рекурсий от внешнего треугольника до самых внутренних (которые, собственно, и отображаются на экране), но вторая рекурсия обходится достаточно дешево по сравнению с процессом отображения, так что цена подобной гибкости оказывается вполне приемлемой.
Генерация и отображение ландшафта
После такого внушительного пролога код для генерации ландшафта выглядит на удивление просто. Процедура FractureTriangle() (см. листинг 8.2) получает треугольник и количество остающихся итераций Plys. Если Plys превышает 1, FractureTriangle() вызывает FractureLine() для расчета (или получения готовых) высот середин отрезков, а затем вызывает себя для каждого из четырех треугольников, которые получаются после разделения. FractureLine() вызывает Midpoint() (обе процедуры приведены в листинге 8.2), чтобы вычислить среднюю точку отрезка, образованного двумя вершинами, и затем смотрит, была ли ее высота задана ранее. Если середина еще не инициализирована, FractureLine() изгибает отрезок, поднимая или опуская его середину.После того как ландшафт будет рассчитан, FL3 отображает его в текущем окне и в текущем режиме отображения с помощью кода, приведенного в листинге 8.3. При изменении размеров окна или режима отображения FL3 перерисовывает ландшафт.
Листинг 8.3. Модуль DISPLAY.PAS
unit Display;
{ Fractal Landscapes 3.0 -
Copyright © 1987..1997, Джон Шемитц }
interface
uses WinTypes, WinProcs,
SysUtils, Graphics, Forms,
Global, Database;
const
DrawingNow: boolean = False;
AbortDraw: boolean = False;
type
EAbortedDrawing = class (Exception) end;
procedure ScreenColors;
procedure PrinterColors;
procedure DrawTriangle( Canvas: TCanvas;
const A, B, C: TVertex;
Plys: word;
PointDn: boolean);
procedure DrawVerticals(Canvas: TCanvas);
{$ifdef Debug}
const DebugString: string = '';
{$endif}
implementation
uses Main;
type
Surfaces = record
Outline, Fill: TColor;
end;
const
scrnLand: Surfaces = (Outline: clLime;
Fill: clGreen);
scrnWater: Surfaces = (Outline: clBlue;
Fill: clNavy);
scrnVertical: Surfaces = (Outline: clGray;
Fill: clSilver);
prnLand: Surfaces = (Outline: clBlack;
Fill: clWhite);
prnWater: Surfaces = (Outline: clBlack;
Fill: clWhite);
prnVertical: Surfaces = (Outline: clBlack;
Fill: clWhite);
var
Land, Water, Vertical: Surfaces;
procedure ScreenColors;
begin
Land := scrnLand;
Water := scrnWater;
Vertical := scrnVertical;
end;
procedure PrinterColors;
begin
Land := prnLand;
Water := prnWater;
Vertical := prnVertical;
end;
function Surface(Outline, Fill: TColor): Surfaces;
begin
Result.Outline := Outline;
Result.Fill := Fill;
end;
{ $define Pascal} {$define Float}
{$ifdef Pascal}
{$ifdef Float}
type
TFloatTriple = record X, Y, Z: double; end;
function FloatTriple(T: TTriple): TFloatTriple;
begin
Result.X := T.X / UnitLength;
Result.Y := T.Y / UnitLength;
Result.Z := T.Z / UnitLength;
end;
function Project(const P: TTriple): TPixel;
{ Перспективное преобразование координат точки }
var
Delta_Y: double;
Tr, V: TFloatTriple;
begin
Tr := FloatTriple(P);
V := FloatTriple(VanishingPoint);
Delta_Y := Tr.Y / V.Y;
Result.X := Round( DisplayWidth *
((V.X - Tr.X) * Delta_Y
+ Tr.X));
Result.Y := DisplayHeight -
Round( DisplayHeight *
((V.Z - Tr.Z) * Delta_Y
+ Tr.Z));
end;
{$else}
function Project(const Tr: TTriple): TPixel;
{ Перспективное преобразование
координат точки }
var
Delta_Y: integer;
begin
Delta_Y := MulDiv(Tr.Y, UnitLength,
VanishingPoint.Y);
Result.X := MulDiv( MulDiv
( VanishingPoint.X - Tr.X,
Delta_Y, UnitLength) + Tr.X,
DisplayWidth, UnitLength);
Result.Y := DisplayHeight -
MulDiv( MulDiv( VanishingPoint.Z - Tr.Z,
Delta_Y, UnitLength) + Tr.Z,
DisplayHeight, UnitLength );
end;
{$endif}
{$else}
function Project(const Tr: TTriple): TPixel;
assembler;
{ Перспективное преобразование
координат точки }
asm
{$ifdef Ver80} {Delphi 1.0; 16-bit}
les di,[Tr]
mov si,word ptr UnitLength
{ Масштабный коэффициент }
mov ax,[TTriple ptr es:di].Y{ Tr.Y }
imul si { Умножаем на
LoWord(UnitLength) }
idiv VanishingPoint.Y
{ Scaled(depth/vanishing.depth) }
{DeltaY equ bx }
mov bx,ax
{ Сохраняем Delta.Y }
mov ax,VanishingPoint.Z
sub ax,[TTriple ptr es:di].Z{ Delta.Z }
imul bx
{ Delta.Z * Delta.Y }
idiv si
{ Unscale(Delta.Z * Delta.Y) }
add ax,[TTriple ptr es:di].Z
{ Tr.Z + Unscale(Delta.Z * Delta.Y) }
mov cx,[DisplayHeight]
{ Используем дважды... }
imul cx
{ (Tr.Z+Delta.Z*Delta.Y)*Screen.Row }
idiv si
{ Unscale }
sub cx,ax
{ Px.Y }
mov ax,VanishingPoint.X
sub ax,[TTriple ptr es:di].X
{ Delta.X }
imul bx
{ Delta.X * Delta.Y }
idiv si
{ Unscale(Delta.X * Delta.Y) }
add ax,[TTriple ptr es:di].X
{ Tr.X + Unscale(Delta.X * Delta.Y) }
imul [DisplayWidth]
{ (Tr.X+Delta.X*Delta.Y)*Screen.Col}
idiv si
{ Px.X := Unscale(см. выше) }
mov dx,cx
{Возвращаем (X,Y) в ax:dx}
{$else} {Delphi 2.0 or better; 32-bit}
push ebx
{ Delphi 2.0 требует, чтобы }
push esi
{ значения этих регистров }
push edi
{ были сохранены }
mov edi,eax
{ lea edi,[Tr]}
push edx
{ Сохраняем @Result }
mov si,word ptr UnitLength
{ Масштабный коэффициент }
mov ax,TTriple[edi].Y
{ Tr.Y }
imul si
{ Умножаем на }
{ LoWord(UnitLength) }
idiv VanishingPoint.Y
{ отношение глубины текущей
точки к глубине точки
перспективы}
{DeltaY equ bx }
mov bx,ax
{ Сохраняем Delta.Y }
mov ax,VanishingPoint.Z
sub ax,TTriple[edi].Z
{ Delta.Z }
imul bx
{ Delta.Z * Delta.Y }
idiv si
{ Unscale(Delta.Z * Delta.Y) }
add ax,TTriple[edi].Z
{ Tr.Z + Unscale(Delta.Z * Delta.Y) }
mov cx,[DisplayHeight]
{ Используем дважды... }
imul cx
{ (Tr.Z+Delta.Z*Delta.Y)*Screen.Row }
idiv si
{ Unscale }
sub cx,ax
{ Px.Y }
mov ax,VanishingPoint.X
sub ax,TTriple[edi].X
{ Delta.X }
imul bx
{ Delta.X * Delta.Y }
idiv si
{ Unscale(Delta.X * Delta.Y) }
add ax,TTriple[edi].X
{ Tr.X + Unscale(Delta.X * Delta.Y) }
imul [DisplayWidth]
{ (Tr.X+Delta.X*Delta.Y)*Screen.Col }
idiv si
{ Px.X := Unscale(см. выше) }
// Теперь ax=x, cx=y; мы хотим превратить
//их в longint
// и сохранить в Result
mov ebx,$0000FFFF
and eax,ebx
{ Очищаем старшее слово}
and ecx,ebx
pop edx
{ Восстанавливаем результат }
mov TPixel[edx].X,eax
mov TPixel[edx].Y,ecx
pop edi
pop esi
pop ebx
{$endif}
end;
{$endif}
procedure DrawPixels(const Canvas:
TCanvas;
const A, B, C, D:
TPixel;
const N:
word;
const Surface:
Surfaces);
begin
if AbortDraw then raise
EAbortedDrawing.Create('');
Canvas.Pen.Color := Surface.Outline;
if DrawMode = dmOutline
then if N = 3
then Canvas.PolyLine( [A, B, C, A] )
else Canvas.PolyLine( [A, B, C, D, A] )
else begin
Canvas.Brush.Color := Surface.Fill;
if N = 3
then Canvas.Polygon( [A, B, C] )
else Canvas.Polygon( [A, B, C, D] )
end;
end;
procedure CalcCrossing(var Low, High, Crossing:
TTriple; SetLow: boolean);
var
CrossOverRatio: LongInt;
begin
CrossOverRatio := (SeaLevel - Low.Z) *
UnitLength div (High.Z - Low.Z);
{ Расстояние от точки пересечения до A
рассчитывается как отношение }
{ длины отрезка к полной длине AB,
умноженное на UnitLength }
Crossing := Triple( Low.X + Unscale
((High.X - Low.X) *
CrossOverRatio),
Low.Y + Unscale((High.Y - Low.Y) *
CrossOverRatio),
SeaLevel );
if SetLow then Low.Z := SeaLevel;
end;
procedure DrawVertical(Canvas:
TCanvas; const A, B: TTriple;
var pA, pB: TPixel);
var
pC, pD: TPixel;
tC, tD: TTriple;
begin
tC := A;
tC.Z := SeaLevel;
pC := Project(tC);
tD := B;
tD.Z := SeaLevel;
pD := Project(tD);
DrawPixels(Canvas, pA, pB, pD, pC, 4, Vertical);
end;
procedure DrawVerticals(Canvas: TCanvas);
type
Triad = record
T: TTriple;
V: TVertex;
P: TPixel;
end;
var
Work: Triad;
procedure Step( const Start: TVertex;
var Front: Triad;
var StepDn: GridCoordinate
);
var
Idx: word;
Back, Interpolate: Triad;
begin
Back.V := Start;
Back.T := GetTriple(Back.V);
if Back.T.Z > SeaLevel then Back.P
:= Project(Back.T);
for Idx := 1 to EdgeLength do
begin
Front.V := Back.V;
Inc(Work.V.BC);
Dec(StepDn);
Front.T := GetTriple(Front.V);
if Front.T.Z > SeaLevel then Front.P
:= Project(Front.T);
case (ord(Back.T.Z > SeaLevel) shl 1) +
ord(Front.T.Z > SeaLevel) of
1: begin { Задняя точка ниже
уровня моря, передняя - выше }
CalcCrossing(Back.T, Front.T,
Interpolate.T, False);
Interpolate.P := Project
(Interpolate.T);
DrawVertical(Canvas,
Interpolate.T, Front.T,
Interpolate.P, Front.P);
end;
2: begin { Задняя точка выше
уровня моря, передняя - ниже }
CalcCrossing(Front.T, Back.T,
Interpolate.T, False);
Interpolate.P := Project(Interpolate.T);
DrawVertical(Canvas, Back.T, Interpolate.T,
Back.P, Interpolate.P);
end;
3: DrawVertical(Canvas, Back.T, Front.T,
Back.P, Front.P);
{ Обе точки выше уровня моря }
end;
Back := Front;
end;
end;
begin
Step(C, Work, Work.V.AB );
Step(B, Work, Work.V.CA );
end;
function InnerProduct({const} A,
B: TTriple): LongInt;
begin
InnerProduct := IMUL(A.X, B.X) +
IMUL(A.Y, B.Y) +
IMUL(A.Z, B.Z) ;
end;
function Delta(A, B: TTriple): TTriple;
begin
Result := Triple(A.X - B.X, A.Y -
B.Y, A.Z - B.Z);
end;
function LandColor(const A, B, C: TTriple):
TColor;
var
Center, ToA, ToLight: TTriple;
Cos, Angle: double;
GrayLevel: integer;
begin
Center := Triple( (A.X + B.X + C.X) div 3,
(A.Y + B.Y + C.Y) div 3,
(A.Z + B.Z + C.Z) div 3 );
ToA := Delta(A, Center);
ToLight := Delta(Center, LightSource);
{$ifopt R-} {$define ResetR} {$endif}
{$R+}
try
Cos := InnerProduct(ToA, ToLight) /
(Sqrt({Abs(}InnerProduct(ToA, ToA){)}) *
Sqrt({Abs(}InnerProduct(ToLight, ToLight){)}) );
try
Angle := ArcTan (Sqrt (1 - Sqr (Cos)) / Cos);
except
on Exception do Angle := Pi / 2; {ArcCos(0)}
end;
{$ifdef HighContrast}
GrayLevel := 255 - Round(255 * (Abs(Angle) /
(Pi / 2)));
{$else}
GrayLevel := 235 - Round(180 * (Abs(Angle) /
(Pi / 2)));
{$endif}
except
on Exception {любое исключение} do GrayLevel
:= 255; { Деление на 0... }
end;
{$ifdef ResetR} {$R-} {$undef ResetR} {$endif}
Result := PaletteRGB(GrayLevel, GrayLevel,
GrayLevel);
end;
procedure Draw3Vertices( Canvas: TCanvas;
const A, B, C: TVertex; Display: boolean);
var
Color: TColor;
pA, pB, pC, pD, pE: TPixel;
tA, tB, tC, tD, tE: TTriple;
aBelow, bBelow, cBelow: boolean;
begin
tA := GetTriple(A); tB := GetTriple(B);
tC := GetTriple(C);
{$ifdef FloatingTriangles}
ta.z := ta.z + random(Envelope shr Plys) -
random(Envelope shr Plys);
tb.z := tb.z + random(Envelope shr Plys) -
random(Envelope shr Plys);
tc.z := tc.z + random(Envelope shr Plys) -
random(Envelope shr Plys);
{$endif}
aBelow := tA.Z <= SeaLevel;
bBelow := tB.Z <= SeaLevel;
cBelow := tC.Z <= SeaLevel;
case ord(aBelow) + ord(bBelow) + ord(cBelow) of
0: if Display then
{ Все вершины выше уровня моря }
begin
pA := Project(tA);
pB := Project(tB);
pC := Project(tC);
if DrawMode = dmRender
then begin
Color := LandColor(tA, tB, tC);
DrawPixels( Canvas,
pA, pB, pC, pC, 3,
Surface(Color, Color));
end
else DrawPixels( Canvas,
pA, pB, pC, pC, 3, Land);
end;
3: if Display then { Все вершины ниже
уровня моря }
begin
tA.Z := SeaLevel;
tB.Z := SeaLevel;
tC.Z := SeaLevel;
pA := Project(tA);
pB := Project(tB);
pC := Project(tC);
DrawPixels( Canvas, pA, pB, pC, pC, 3,
Water);
end;
2: begin { Одна вершина над водой }
{ Сделаем так, чтобы это была вершина tA }
if aBelow then
if bBelow
then SwapTriples(tA, tC)
else SwapTriples(tA, tB);
CalcCrossing(tB, tA, tD, True);
CalcCrossing(tC, tA, tE, True);
pA := Project(tA); pB := Project(tB);
pC := Project(tC);
pD := Project(tD); pE := Project(tE);
DrawPixels( Canvas, pD, pB, pC, pE, 4,
Water);
if Drawmode = dmRender
then begin
Color := LandColor(tD, tA, tE);
DrawPixels( Canvas, pD, pA, pE,
pE, 3,
Surface(Color, Color));
end
else DrawPixels( Canvas, pD, pA, pE, pE,
3, Land);
end;
1:begin { Одна вершина под водой }
{ Сделаем так, чтобы это была
вершина tA }
if bBelow
then SwapTriples(tA, tB)
else if cBelow then
SwapTriples(tA, tC);
CalcCrossing(tA, tB, tD, False);
CalcCrossing(tA, tC, tE, True);
pA := Project(tA); pB := Project(tB);
pC := Project(tC);
pD := Project(tD); pE := Project(tE);
DrawPixels( Canvas, pD, pA, pE, pE,
3, Water);
if DrawMode = dmRender
then begin
Color := LandColor(tD, tB,
tC);
DrawPixels( Canvas,
pD, pB, pC, pE, 4,
Surface(Color, Color));
end
else DrawPixels( Canvas, pD, pB, pC, pE, 4, Land);
end;
end;
end;
procedure DrawTriangle( Canvas: TCanvas;
const A, B, C: TVertex;
Plys: word;
PointDn: boolean);
var
AB, BC, CA: TVertex;
begin
if Plys = 1
then Draw3Vertices(Canvas, A, B, C,
(DrawMode <> dmOutline) OR PointDn)
else
begin
AB := Midpoint(A, B);
BC := Midpoint(B, C);
CA := Midpoint(C, A);
if Plys = 3
then FractalLandscape.DrewSomeTriangles(16);
Dec(Plys);
if PointDn
then begin
DrawTriangle(Canvas, CA, BC, C, Plys, True);
DrawTriangle(Canvas, AB, B, BC, Plys, True);
DrawTriangle(Canvas, BC, CA, AB, Plys, False);
DrawTriangle(Canvas, A, AB, CA, Plys, True);
end
else begin
DrawTriangle(Canvas, A, CA, AB, Plys, False);
DrawTriangle(Canvas, BC, CA, AB, Plys, True);
DrawTriangle(Canvas, CA, C, BC, Plys, False);
DrawTriangle(Canvas, AB, BC, B, Plys, False);
end;
end;
end;
begin
ScreenColors;
end.
Отображение ландшафта может выполняться в трех режимах: каркасном (Outline), c заполнением (Filled) и со светотенью (rendered). В любом из этих режимов ландшафт рисуется как набор треугольников, при этом координаты отдельных вершин TTriple с помощью простого перспективного преобразования пересчитываются в экранные пиксели TPixel, а затем получившийся треугольник рисуется с помощью функции PolyLine или Polygon. Единственное отличие между режимами заключается в том, что в каркасном режиме рисуется обычная «проволочная сетка» без отсечения невидимых линий, а в двух последних режимах порядок вывода и заполнение прямоугольников обеспечивают отсечение невидимых линий методом «грубой силы» (иногда это называется «алгоритмом маляра»). В свою очередь режим со светотенью отличается тем, что цвет каждого треугольника в нем зависит от угла, под которым данная грань расположена по отношению к «солнцу».
Чтобы увеличить правдоподобие изображения, в Draw3Vertices() реализована упрощенная концепция «уровня моря». Любой треугольник, полностью находящийся над уровнем моря, рисуется нормально, а любой треугольник, полностью погруженный в воду, рисуется синим цветом на уровне моря. Если треугольник пересекает уровень моря, FL3 интерполирует точки пересечения, после чего отдельно рисует надводную и подводную части. Хотя для «побережий» такая методика вполне приемлема, с «озерами» дело обстоит сложнее: FL3 рисует воду лишь в тех местах, которые находятся ниже уровня моря.
После завершения прорисовки всех треугольников FL3 рисует вертикальные линии вдоль двух передних краев от уровня моря до всех вершин, которые находятся над водой. Эти линии особенно полезны в заполненном и светотеневом режимах — непрозрачные вертикальные грани будут скрывать «внутреннюю» структуру поверхности.
Процедура Project()
Проекционная процедура Project() — «рабочая лошадка», от которой зависят все операции графического вывода. Она преобразует трехмерные координаты TTriple в плоские TPixel с использованием одноточечной перспективы и текущих размеров окна.Фактически эта процедура проводит линию
между двумя точками — текущей и точкой перспективы — и определяет, где
эта линия пересекается с плоскостью экрана. Сложность листинга 8.3 обусловлена
использованием вычислений с фиксированной точкой. (В основном это наследство,
доставшееся программе FL3 от ее первых версий, появившихся в те дни, когда
вычисления с плавающей точкой были очень медленными. С другой стороны,
вычисления с фиксированной точкой сокращают размер базы данных вершин и
позволяют разместить всю базу в одном сегменте данных.) Если отказаться
от математики с фиксированной точкой, мы получим следующее:
function Project(const P: TTriple): TPixel;
{ Трехмерное преобразование точки }
var
Delta_Y: double;
Tr, V: TFloatTriple;
begin
Tr := FloatTriple(P);
V := FloatTriple(VanishingPoint);
Ratio := Pt.Y / V.Y;
Result.X := Round( DisplayWidth *
((V.X - Pt.X) * Ratio + Pt.X));
Result.Y := DisplayHeight -
Round( DisplayHeight *
((V.Z - Pt.Z) * Ratio + Pt.Z));
end;
Процедура вычисляет отношение глубины точки к глубине точки перспективы и умножает его на разности координат этих точек по осям x и z. Поскольку координаты TTriple принадлежат интервалу 0…1, для получения экранных координат можно просто умножить спроектированные координаты на размер окна.
Каркасный режим
Из всех режимов отображения проще всего реализован каркасный режим. В нем рисуются лишь контуры треугольников: «земля» — зеленым цветом, а «вода» — синим. Если здесь что и заслуживает внимания, так это простота и изящество реализации DrawPixels() в Delphi. В API-версии DrawPixels() (написанной на C или Borland Pascal) вместо одного простого вызова Canvas.Polyline ([A, B, C, A]) пришлось бы объявлять локальный массив и выполнять четыре присваивания — не говоря уже о хлопотах, связанных с созданием и уничтожением контекстов устройств (DC) Windows и графических перьев.Режим с заполнением
Каркасный режим работает относительно быстро и неплохо обрисовывает общую структуру поверхности, но обладает большим недостатком: сетка получается прозрачной. Другими словами, задний склон холма виден сквозь передний.В серьезных графических приложениях используются сложные алгоритмы «отсечения скрытых линий», но FL3 не является серьезным приложением и убирает скрытые линии методом «грубой силы», рисуя поверх них (см. рис. 8.2).
Другими словами, DrawTriangle()
сначала рисует задние треугольники, чтобы передние треугольники рисовались
позже и закрывали их. При исходном вызове DrawTriangle() этой процедуре
передается треугольник, расположенный «вершиной вниз» — вершина A
расположена спереди, в нижней части окна, а вершины B и С
— сзади, ближе к верхней части окна (см. рис. 8.8). Следовательно, фрагмент
DrawTriangle(Canvas, CA, BC, C, Plys, True); DrawTriangle(Canvas, AB, B, BC, Plys, True); DrawTriangle(Canvas, BC, CA, AB, Plys, False); DrawTriangle(Canvas, A, AB, CA, Plys, True);
сначала рисует левый субтреугольник, а затем — правый. Ориентация этих «внешних» субтреугольников совпадает с ориентацией треугольника ABC, а порядок перечисления параметров в рекурсивных вызовах DrawTriangle() гарантирует, что новая точка A будет расположена спереди, а точки B и C — сзади.
Третья строка вызов рисует «внутренний» субтреугольник, который визуально находится перед вторым (правым верхним) треугольником. Внутренний субтреугольник всегда перевернут по отношению к своему внешнему треугольнику, поэтому при вызове DrawTriangle() он располагается «вершиной вверх». Порядок перечисления параметров гарантирует, что при таком вызове вершина A остается сзади, а B и C — спереди, в нижней части экрана. Если вы просмотрите набор рекурсивных вызовов, соответствующих ветви not PointDn в процедуре DrawTriangle(), то увидите, что расположенные «вершиной вверх» треугольники рисуются в порядке «сзади вперед, справа налево»1.
Четвертый вызов DrawTriangle() рисует последний, передний субтреугольник.
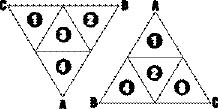
Рис. 8.8. Порядок рисования и ориентация треугольников
Режим со светотенью
В светотеневом режиме мы пытаемся воспроизвести изображение более реалистично и выбираем цвет каждого треугольника в зависимости от угла между его поверхностью и лучами «солнца». Треугольники, расположенные перпендикулярно лучам, выглядят светлее тех, что расположены под углом (см. рис. 8.3). Хотя светотень, например, хорошо показывает структуру поверхности речного русла, в целом пейзаж выглядит… слишком серым. Вы можете поэкспериментировать с палитрой и написать свою функцию LandColor(), чтобы сделать изображение псевдоцветным.Создавайте собственные миры
FL3 демонстрирует принципы построения простейших фрактальных ландшафтов. Возможно, вам захочется улучшить распределение случайных чисел, изменить блок визуализации или модифицировать алгоритм для создания целых фрактальных планет.С первого взгляда трудно понять, что «плазменные» алгоритмы представляют собой разновидность того же алгоритма построения фрактальных ландшафтов: вместо треугольников в них делятся прямоугольники, а третье измерение отображается с помощью цвета, а не перспективы.
Полный исходный текст программы FL3 вместе
со всеми файлами Delphi 3, необходимыми для ее компиляции и запуска, находится
на CD-ROM в каталоге этой главы.