Таинственный модуль Math 

Исследуем новый модуль Delphi, о котором мало кто знает, а заодно попробуем переложить на него всю черную работу по статисти ческой обработке данных.

Вторая и третья версии Delphi содержат первоклассный вспомогательный модуль, которому до сих пор не уделялось должного внимания. Он докумен тирован (в некотором роде), о его существовании знают (по крайней мере некоторые), но почти никто понятия не имеет о том, как им правильно пользоваться. Этот модуль называется Math и содержит превосходный набор финансовых, статистических и общих арифметических и тригонометрических функций. 

В этой главе я покажу вам, как, используя некоторые из этих функций, построить (и использовать) связанный с данными компонент статистической обработки TDBStatistics. С помощью этого компонента вы сможете выдать своим пользователям полную статистическую сводку по более чем 13показателям. 

Три веских довода в пользу модуля Math 

Во-вторых, использование статистических средств SQL неприемлемо. SQL содержит всего лишь четыре или пять статистических функций — слишком мало для получения полной статистической картины. 

В-третьих, выбор модуля Math вместо решений, основанных на SQL или BDE, гарантирует работу компонента TDBStatistics с другими механизмами баз данных (например, Apollo, Titan или Direct Access). 

Динамические данные и статические объявления

const Data: array of Double 

Использование таких функций осложняется тем, что массив, передаваемый подобным образом, должен быть объявлен статическ и. С первого взгляда кажется, что передать этим функциям динамические данные невозможно. Большинство программистов находят для дилеммы динамических данных два обходных пути. Они: 

1.  
2. «Зашивают» данные в программу (жесткое кодирование). 
3. Создают огромный массив и надеются, что пользователь не выйдет за его пределы.

Mean([3, 2, 1, 5, 6]); 

Фактически эта строка представляет собой калькулятор, который всегда выдает один и тот же результат. Не слишком полезный вариант, не правда ли¹? 

Понятно, что жесткое кодирование не решает проблем. Остается объявление массива «с запасом». Хотя в некоторых ситуациях такая методика чрезвычайно полезна (а иногда даже необходима), она может приводить к непредвиденным осложнениям. 

Это особенно справедливо для модуля Math. Снова рассмотрим функцию Mean. «Среднее арифметическое» определяется как сумма N чисел, деленная на N. Предположим, у нас имеется массив из 10 000 элементов, который мы собираемся передать функции Mean. Если пользователь введет значения только для 50 элементов, знаменатель (N) будет по-прежнему равен 10 000 и превысит правильное значение на 9 950! Как говорится, приплыли… 

Slice спешит на помощь 

function Slice(var A: array; Count: Integer): array; 

Slice получает массив любого размера и тип и возвращает Count элементов так, словно они являются отдельным и независимым массивом. С помощью Slice можно объявить очень большой массив и использовать в нем лишь
нужное количество элементов. 

Функция Slice возрождает идею объявления «с запасом», но на этот раз нам уже не придется заботиться о неправильном знаменателе. А это в свою очередь позволит передавать функциям динамические данные. 

Вооружившись новыми знаниями, мы переходим к созданию быстрого и удобного компонента для статистической обработки данных. 

Создание компонента DBStatistics 

Определение задач компонента 

Построение компонента желательно начать с определения тех задач, которые он должен решать. Наверное, вы догадались, что сейчас мы займемся именно этим применительно к DBStatistics. 

Главная задача DBStatistics — предоставлять простой доступ к одному, нескольким или всем 13 статистическим показателям после задания имени поля и источника данных. Для этого компоненту понадобится следующее: 

1. Доступ к данным, желательно через стандартный источник данных (DataSource). 
2. Место для локального хранения больших объемов данных. 
3. Способ извлечения данных из источника. 
4. Способ удобного получения любого из 13 статистических показателей.

Получение доступа к данным 

fDataSource : TDataSource; 

Свойство DataSource, предоставляющее доступ к этому полю, конечно, становится доступным в режиме разработки благодаря ключевому слову published. 

Кроме того, DBStatistics необходимо сообщить о том, какое поле следует анализировать. Это легко достигается с помощью свойства DataField. Во всем этом нет ничего нового, эти свойства можно найти в любом компоненте на вкладке Data Controls. Поскольку эти свойства так часто встречаются, включение их в DBstatistics помогает создать более знакомую обстановку в режиме разработки. Локальное хранение данных

После получения доступа к данным нам потребуется место для их хранения. Процедуры модуля Math работают со статически объявленными массивами; следовательно, нам понадобится такой массив. Мы назовем его Data. 

Остается вопрос: каким должно быть максимальное количество элементов в Data? При выборе этого значения приходится учитывать два фактора. Первый фактор — количество записей в таблице среднего (для ваших приложений) размера. Если объем таблицы обычно не превышает 4000 записей, то максимальное количество элементов вполне можно выбрать равным 4500. 

Второй фактор — объем доступной памяти. Если расход памяти непринци пиален, массив можно сделать сколь угодно большим. В противном случае оптимальный размер приходится искать методом проб и ошибок. 

В нашем примере объявляется массив Data, состоящий из 10 000 элементов (разумеется, значение 10 000 объявлено в виде константы — MaxValues). Для большинства типичных приложений этого вполне достаточно. 

Извлечение данных 

Однако в случае TDBStatistics все оказывается несколько сложнее. Так как пользователь может захотеть проанализировать набор записей, превышающий границы нашего массива, мы должны позволить ему выбрать подмножество данных. Для этого используются два свойства: UpperBound и LowerBound. Они предоставляют компоненту информацию о начальной и конечной записях набора. Следовательно, процедура проверки должна следить за этими двумя величинами. Самый простой выход заключается в использовании функции, которая: 

1. Проверяет правильность свойств; 
2. Вносит необходимые поправки; 
3. Возвращает разность (с учетом поправок) между UpperBound и LowerBound.

LowerBound + 1:
if (LowerBound < 1) then
   LowerBound := 1;
if (UpperBound < 1) then
   UpperBound := LowerBound + 1;

ALIGN="JUSTIFY">Следующая проверка убеждает в том, что UpperBound больше, чем LowBound. Если выясняется обратное, значения LowBound и UpperBound меняются местами:

if (LowerBound > UpperBound) then
begin
     TempInt := UpperBound;
     UpperBound := LowerBound;
     LowerBound := TempInt;
end;

Затем мы проверяем, не превышают ли UpperBound и LowerBound количество записей в источнике (то есть значение DataSource.DataSet.RecordCount, извлечен ное ранее и сохраненное в переменной Records), и при необходимости исправляем их:

if (LowerBound > Records) then
   LowerBound := 1;
if (UpperBound > Records) then
   UpperBound := Records;

При последней проверке мы убеждаемся в том, что разность между UpperBound и LowerBound не превышает количества элементов в массиве Data. Другими словами, количество сохраняемых элементов не должно превышать размер массива:

if (UpperBound - LowerBound > MaxValues) then
   UpperBound := LowerBound + MaxValues;

Наконец, функция GetRange возвращает разность между проверенными и исправленными значениями 

UpperBound и LowerBound:
Result := UpperBound - LowerBound;

Так в нашем случае выполняется проверка ошибок. 

После завершения проверки можно переходить к извлечению данных из источника и их сохранению в массиве Data. Это происходит в процедуре FillArray. 

Настоящая работа FillArray начинается с вызова GetRange. Затем, после проверки границ (см. выше), можно извлечь данные и сохранить их в локальном массиве. Сначала мы открываем источник данных и переходим к записи, номер которой задается свойством 

LowerBound:
fDataSource.DataSet.Open;
fDataSource.DataSet.MoveBy(LowerBound);

Затем мы проверяем тип fDataField. Если поле содержит числовые значения, мы читаем данные, запись за записью, и помещаем их в массив Data:

if ((fDataSource.DataSet.FieldByName(fDataField) 
is TCurrencyField) or
(fDataSource.DataSet.FieldByName(fDataField) is 
TFloatField) or
(fDataSource.DataSet.FieldByName(fDataField) is 
TIntegerField) or
(fDataSource.DataSet.FieldByName(fDataField) is 
TSmallIntField))then
begin
  for i := LowerBound to UpperBound do
  begin
    if not (fDataSource.DataSet.FieldByName
    (fDataField).IsNull) then
       Data[Index] :=
           fDataSource.DataSet.FieldByName
           (fDataField).Value
    else
           Data[Index] := 0;
    Inc(Index);
    fDataSource.DataSet.Next;
  end;
end

Из символьных полей данные извлекаются несколько иначе. Единственный вид символьных данных, с которыми умеет работать наш компонен т, — это ZIP-коды¹. Существует два типа ZIP-кодов: старые, состоящие из пяти цифр, и новые, «пять плюс четыре». 

С точки зрения TDBStatistics ZIP-коды из пяти цифр можно преобразовать в числовой тип без дальнейшей обработки. Если значение состоит из девяти цифр и включает дефис, то дефис необходимо предварительно заменить символом «точка» (.), чтобы поле можно было привести к числовому типу:

else if (fDataSource.DataSet.FieldByName
(fDataField) is TStringField)
  then
  begin
    for i := LowerBound to UpperBound do
      begin
 TempString :=
   fDataSource.DataSet.FieldByName
   (fDataField).Value;
 if (Pos('-', TempString) > 0) then
   TempString[Pos('-', TempString)] := '.';
 Data[Index] := StrToFloat(TempString);
 Inc(Index);
 fDataSource.DataSet.Next;
      end;
  end;

Наконец, мы закрываем источник данных и сбрасываем два флага: 

fDataSource.DataSet.Close; 

IsArrayFilled := True; 

DidGetAll := False; 

Переменная IsArrayFilled позволяет другим методам компонента узнать, были ли извлечены данные из источника. Если она равна False, другие процедуры могут вызвать FillArray перед тем, как начинать свою работу. Переменная DidGetAll — другой флаг, используемый методами доступа (его смысл разъясняется ниже). 

Статистическая обработка 

1. Метод, извлекающий все 13 показателей сразу; 
2. Отдельные методы доступа для каждого из 13 результатов, доступ к которым осуществляется с помощью свойств.

Для одновременного получения всех показателей используется процедура GetAllStats. Она передает массив Data всем 13 статистическим функциям и сохраняет результаты в переменных, определенных в секции private нашего компонента. Кроме того, флагу DidGetAll присваивается True — это показывает другим методам, что все статистические показатели уже получены. 

Разумеется, отдельные методы доступа могут проверять значение DidGetAll. Если оно равно True, метод доступа просто возвращает ранее сохраненную величину. С другой стороны, если флаг DidGetAll равен False, метод доступа может вызвать соответствующую функцию модуля Math напрямую и вернуть полученный результат. В качестве примера типичного метода доступа мы рассмотрим метод GetMean, который возвращает среднее арифметическое для поля DataField из выбранного диапазона записей. 

Прежде всего необходимо позаботиться о том, чтобы данные были получены из источника и сохранены в массиве 

Data:
if not (IsArrayFilled) then
   FillArray;

Затем следующая проверка — на этот раз необходимо убедиться, что искомый статистический показатель не был вычислен раньше. Если результат уже был получен и сохранен, нет смысла вычислять его заново — метод доступа просто возвращает сохраненное значение для экономии времени. 

С другой стороны, если среднее арифметическое еще не вычислялось, мы вызываем соответствующую функцию модуля Math с использованием функций Slice и GetRange. В итоге мы возвращаем значение, полученное от модуля Math:

if not (DidGetAll) then 

fMean := Math.Mean(Slice(Data,GetRange)); 

Result := fMean; 

Теперь мы располагаем быстрым и удобным способом получения любого статистического показателя и можем вставить TDBStatistics в любой проект. 

Тестирование компонента DBStatistics 

Все файлы этого проекта находятся на CD-ROM, в подкаталоге главы 11. В тексте будет приведен лишь непосредственно обсуждаемый код. 

Обратите внимание: эта форма выглядит стандартно — на ней есть несколько самых обычных визуальных элементов, а также компоненты TTable, TDataSource, TOpenDialog и, разумеется, TDBStatistics. При запуске StatsProject пользователь должен прежде всего выбрать таблицу. Это делается с помощью кнопки BtnTableSelect — элемента TButton с надписью «1. Select a table & field». В обработчике события OnClick кнопки BtnTableSelect имя таблицы определяется с помощью компонента OpenDialog1 класса TOpenDialog. 

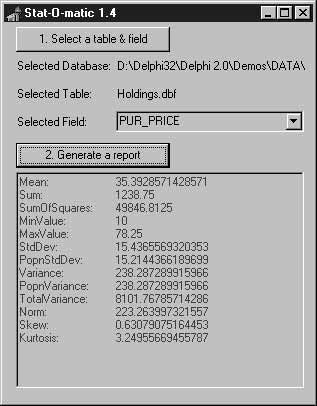
Рис. 11.1. Программа StatsProject во время выполнения

Все начинается с вызова метода Execute. Если был выбран файл с допусти мым именем, работа продолжается:

with OpenDialog1 do
   begin
      Execute;
      if FileName = '' then
        exit;

Затем мы устанавливаем свойства компонента TTable в соответствии с файлом, выбранного пользователем, и выводим сведения о файле с помощью двух элементов TLabel:

Table1.DatabaseName := ExtractFilePath(FileName);
LblDatabase.Caption := ExtractFilePath(FileName);
Table1.TableName := ExtractFileName(FileName);
LblTable.Caption := ExtractFileName(FileName);

Поскольку TDBStatistics обрабатывает данные лишь из одного поля, мы должны обеспечить пользователя средствами для выбора поля. Для этого мы извлекаем имена всех полей из TTable и включаем их в список:

CBFields.Items.Clear;
CBFields.Text := '';
Memo1.Text := '';
Table1.Open;
for i := 0 to Table1.FieldDefs.Count-1  do
begin
Application.ProcessMessages;
CBFields.Items.Add(Table1.Fields[i].FieldName);
end;
Table1.Close;

На этом выбор таблицы и имени поля завершается. 

После того как пользователь выбрал анализируемое поле, он может сгенерировать статистический отчет в элементе Memo, нажимая кнопку BtnReports (кнопка с надписью «2. Generate a report»). В обработчике BtnReports.OnClick мы прежде всего задаем соответствующие свойства компонента DBStatistics1:

DBStatistics1.LowerBound := 1;
Table1.Open;
DBStatistics1.UpperBound := Table1.RecordCount;
Table1.Close;
DataSource1.DataSet := Table1;
DBStatistics1.DataSource := DataSource1;
DBStatistics1.DataField := CBFields.Text; 
{выбранное поле}

Затем мы вызываем DBStatistics1.GetAllStats и выводим результаты в элементе Memo:

DBStatistics1.GetAllStats;
Memo1.Text := '';
Memo1.Lines.Add('Mean: ' + #09 + #09 +
                FloatToStr(DBStatistics1.Mean));

{ ... и т. д. ... } 

Memo1.Lines.Add('Kurtosis: ' + #09 + #09 +
FloatToStr
(DBStatistics1.Kurtosis));

Дело сделано — у нас появился работоспособный генератор статистических отчетов. 

Ошибки в модуле Math второй версии Delphi 

Дело вот в чем: в модуле Math Delphi 2 перепутаны функции MinValue и Max Value. MinValue возвращает наибольший элемент массива, а MaxValue — наименьший. Хотя эта ошибка не фатальна, о ней все же следует упомянуть (разумеется, компонент DBStatistics исправляет ее в отношении своих свойств MinValue и MaxValue). 

Учтите, что эта ошибка была исправлена в модуле Math, включенном в Delphi 3, а компонент DBStatistics — обновлен с учетом этого. Благодаря нескольким разумным директивам {$IFDEF} компонент TDBStatistics правильно работает и с Delphi 2, и с Delphi 3. 

Пропавшая функция Poly 

Что же делает эта загадочная функция? Выглядит она так: 

function Poly(X: Extended; const Coefficients: array of Double):
Extended; 

Функция Poly предназначена для вычисления полиномов. Единственное ограничение состоит в том, что это должны быть полиномы лишь одной переменной. Функция Poly получает переменную X, для которой вычисляется полином, и массив коэффициентов. Коэффициенты должны быть упорядочены по возрастанию степеней X. 

Следовательно, для следующего полинома: 

4x⁴ [+ 0x³] _ x² + 3x + 34 

массив коэффициентов должен быть упорядочен так: 

34, 3, _1, 0, 4 

Если бы вам потребовалось снабдить функцию Poly пользовательским интерфейсом, вероятно, получилось бы что-то наподобие программы PolyProject (см. рис. 11.2). 

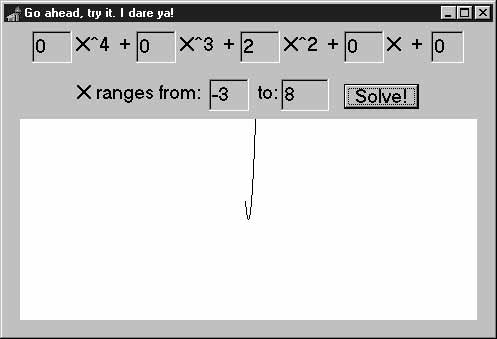
Рис. 11.2. Графическое представление 

Программа PolyProject (она находится на CD-ROM в подкаталоге этой главы) как раз и является таким интерфейсным приложением. Она позволяет задать полином, а затем выводит его график. Обратите внимание — в главном окне программы PolyProject наряду с надписями имеется несколько текстовых полей для ввода коэффициентов полинома. Однако вся основная работа PolyProject выполняется в обработчике события OnClick кнопки Solve!:

procedure TForm1.SolveButtonClick(Sender: 
TObject);
var
   i : Integer;
   XCoes : array[0..4] of double;
   X,Y, OffsetX, OffsetY : Integer;
   NewRect: TRect;

Прежде всего мы заполняем массив XCoes введенными значениями коэффициентов:

begin
     XCoes[0] := StrToFloat(TxtX0.Text);
     XCoes[1] := StrToFloat(TxtX1.Text);
     XCoes[2] := StrToFloat(TxtX2.Text);
     XCoes[3] := StrToFloat(TxtX3.Text);
     XCoes[4] := StrToFloat(Tx1tX4.Text);

После этого необходимо задать начало координат для построения графика. Обычно я использую центр элемента TImage, но при желании можно выбрать любую другую точку:

OffsetX := Image1.Width div 2; 
OffsetY := Image1.Height div 2;

Затем мы инициализируем координату X и очищаем график, заполняя Image1 сплошным белым прямоугольником. Присваивание соответствующего значения свойству Image1.Canvas.Brush.Color гарантирует, что график будет выводиться черным цветом: 

X := 0; { Для надежности инициализируем X } 

NewRect := Rect(0, 0, Image1.Width, Image1.Height); 

Image1.Canvas.Brush.Color := clWhite; 

Image1.Canvas.FillRect(NewRect); 

Image1.Canvas.Brush.Color := clBlack; 

Пора заняться вычислениями. Сначала мы определяем положение начальной точки графика. До входа в цикл for мы ничего не рисуем, просто перед любым серьезным рисованием необходимо установить «перо» в исходную позицию. Затем мы вызываем функцию Poly, передавая ей значение из текстового поля с нижней границей диапазона (TxtRangeStart) и массив XCoes:

with Image1.Canvas do
  begin
    Y := Trunc(Poly(StrToInt(TxtRangeStart.Text), 
    XCoes));
...

Возможно, вы удивитесь тому, что я округляю результат функции Poly. Это делается исключительно для рисования: функция Poly возвращает значение с плавающей точкой (тип Extended), а Windows API работает только с целыми координатами. 

Полученный результат преобразуется в пару (X, Y), которая соответствует нашей центральной точке, после чего «перо» перемещается в эту точку:

X := StrToInt(TxtRangeStart.Text) + OffsetX;
Y := OffsetY - Y;
MoveTo(X,Y);

Затем мы перебираем значения X из заданного интервала, начиная с нижней границы +1 (я только что упоминал о нижней границе) и вплоть до значения верхней границы из соответствующего текстового поля (TxtRangeEnd):

for i := StrToInt(TxtRangeStart.Text) + 1 to
StrToInt(TxtRangeEnd.Text) do
  begin
    Y := Trunc(Poly(I, XCoes));
    X := I + OffsetX;
    Y := OffsetY - Y;
    LineTo(X,Y);
    MoveTo(X,Y);
  end;

Хотя функция Poly является единственной общедоступной , но недокумен тированной функцией модуля Math, в секции implementation можно найти еще несколько интересных процедур (одна из них, например, определяет, является ли величина A «бесконечно малой» по отношению к B!). Ограниченный объем главы не позволяет мне рассказать о них подробнее, но я бы порекомендовал изучить эти функции, если у вас есть исходные тексты и, конечно, терпение! 

То, чего не было в Паскале 

В модуле Math появилось то, чего никогда не было в Паскале — «официаль ная» функция для возведения в степень. Более того, модуль Math содержит сразу две такие функции. 

Первая из них, Power, получает два параметра типа Extended — основание и показатель степени. Вторая функция, IntPower, получает один параметр типа Extended (основание) и один целый параметр (показатель степени). 

Отличия между ними заключаются в том, что функция IntPower, как и многие функции модуля Math, написана целиком на оптимизированном ассемблере для работы с Pentium FPU, что делает ее достаточно быстрой. 

Если вы не знаете, какую функцию следует использовать в вашем приложении, не огорчайтесь. 

Хотя это нигде не объясняется и не документируется, функция Power сама определяет, является ли показатель степени целым числом. Если это так, Power вызывает IntPower. Если же показатель является числом с плавающей точкой, Power вычисляет результат каноническим способом, через натуральный логарифм и экспоненту. 

Сводка функций модуля Math 

Тригонометрические функции и процедуры 

ArcCosh Гиперболический арккосинус 

ArcSin Арксинус 

ArcSinh Гиперболический арксинус 

ArcTahn Гиперболический арктангенс 

ArcTan2 Арктангенс с учетом квадранта (функция ArcTan, не учитывающая квадрант, находится в модуле System) 

Cosh Гиперболический косинус 

Cotan Котангенс 

CycleToRad Преобразование циклов в радианы 

DegToRad Преобразование градусов в радианы 

GradToRad Преобразование градов в радианы 

Hypot Вычисление гипотенузы прямоугольного треугольника по дли- 
нам катетов 

RadToCycle Преобразование радианов в циклы 

RadToDeg Преобразование радианов в градусы 

RadToGrad Преобразование радианов в грады 

SinCos Вычисление синуса и косинуса угла. Как и в случае SumAndSquares
и MeanAndStdDev, одновременная генерация обеих величин 
происходит быстрее 

Sinh Гиперболический синус 

Tan Тангенс 

Tanh Гиперболический тангенс 

Арифметические функции и процедуры 

Floor Округление вниз 

Frexp Вычисление мантиссы и порядка заданной величины 

IntPower Возведение числа в целую степень. Если вы не собираетесь пользо- 
ваться экспонентами с плавающей точкой, желательно исполь- 
зовать эту функцию из-за ее скорости 

Ldexp Умножение X на 2 в заданной степени 

LnXP1 Вычисление натурального логарифма X+1. Рекомендуется для X,
близких к нулю 

LogN Вычисление логарифма X по основанию N 

Log10 Вычисление десятичного логарифма X 

Log2 Вычисление двоичного логарифма X 

Power Возведение числа в степень. Работает медленнее IntPower, но для 
операций с плавающей точкой вполне приемлемо 

Финансовые функции и процедуры 

FutureValue Будущее значение вложения 

InterestPayment Вычисление процентов по ссуде 

InterestRate Норма прибыли, необходимая для получения заданной 
суммы 

InternalRateOfReturn Вычисление внутренней скорости оборота вложения для 
ряда последовательных выплат 

NetPresentValue Вычисление чистой текущей стоимости вложения для 
ряда последовательных выплат с учетом процентной 
ставки 

NumberOfPeriods Количество периодов, за которое вложение достигнет 
заданной величины 

Payment Размер периодической выплаты, необходимой для пога- 
шения ссуды, при заданном числе периодов, процентной 
ставке, а также текущем и будущем значениях ссуды

PeriodPayment Платежи по процентам за заданный период 

PresentValue Текущее значение вложения 

SLNDepreciation Вычисление амортизации методом постоянной нормы 

SYDepreciation Вычисление амортизации методом весовых коэф- 
фициентов 

Статистические функции и процедуры 

MaxValue Максимальное значение в наборе чисел. В Delphi 2 функция 
возвращает минимальное значение 

Mean Среднее арифметическое для набора чисел 

MeanAndStdDev Одновременное вычисление среднего арифметического и 
стандартного отклонения для набора чисел. Вычисляется 
быстрее, чем обе величины по отдельности 

MinIntValue Минимальное значение в наборе целых чисел. Функция по- 
явилась в Delphi 3, ее не существует в Delphi 2 

MinValue Минимальное значение в наборе чисел. В Delphi 2 функция 
возвращает максимальное значение 

MomentSkewKurtosis Статистические моменты порядков с первого по четвертый, 
а также асимметрия (skew) и эксцесс (kurtosis) для набора
чисел 

Norm Норма для набора данных (квадратный корень из суммы 
квадратов) 

PopnStdDev Выборочное стандартное отклонение. Отличается от обыч- 
ного стандартного отклонения тем, что при вычислениях ис- 
пользуется выборочное значение дисперсии, PopnVariance (см. 
ниже) 

PopnVariance Выборочная дисперсия. Использует «смещенную» формулу 
TotalVariance/n 

RandG Генерация нормально распределенных случайных чисел с за- 
данным средним значением и среднеквадратическим от- 
клонением 

StdDev Среднеквадратическое отклонение для набора чисел 

Sum Сумма набора чисел 

SumsAndSquares Одновременное вычисление суммы и суммы квадратов для на- 
бора чисел. Как и в других функциях модуля Math, обе вели- 
чины вычисляются быстрее, чем по отдельности 

SumInt Сумма набора целых чисел. Функция появилась в Delphi 3, 
ее не существует в Delphi 2 

SumOfSquares Сумма квадратов набора чисел 

TotalVariance «Полная дисперсия» для набора чисел. Это сумма квадратов 
расстояний всех величин от их среднего арифметического 

Variance Выборочная дисперсия для набора чисел. Функция ис- 
пользует «несмещенную» формулу TotalVariance/(n1)